ラグランジュの運動方程式の使い方を簡単な例題を用いて解説します.求めたい対象のエネルギーさえ求まれば,それを代入するだけで機械的に運動方程式を求めることができるのが魅力です.
2.1 ラグランジュの運動方程式
\(n\)個の一般化座標\(q_i(i=1, 2, \cdots, n)\)により表現される対象の運動方程式について考えよう.この対象全体の運動・位置・散逸エネルギーをぞれぞれ\(T\),\(U\),\(F\)とします.また,\(i\)番目の一般化座標に加わっている一般化力を\(\omega_i\)とします.このとき,\(i\)番目の一般化座標の運動方程式は下式となり,この式をラグランジュの運動方程式と呼びます.
\begin{eqnarray}\frac{d}{dt} \left( \frac{\partial T}{\partial \dot q_i} \right )-\frac{\partial T}{\partial q_i}+\frac{\partial F}{\partial \dot q_i}+\frac{\partial U}{\partial q_i}= \omega_i\tag{1}\label{eq1}\end{eqnarray}
ツールとして使うことを考えると,実用上便利ですので散逸エネルギーを含む形のラグランジュの運動方程式を紹介します.
2.2 とりあえず,使ってみよう!
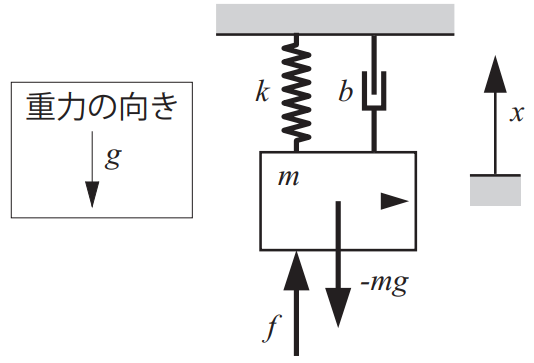
質量\(m\)の質点に剛性\(k\)のばねと粘性\(b\)のダンパが付いており,質点の変位を\(x\)とし,力\(f\)が加わっている場合の質点の運動方程式を導出しよう.一般化座標\(q_1\)に\(x\)を選んだとき,一般化力\(\omega_1\)は\(f\)になります.運動・位置・散逸エネルギーをぞれぞれ\(T\),\(U\),\(F\)を求め,\eqref{eq1}に代入すれば,運動方程式が導出できます.
運動エネルギー\(T\)は下式になります.
\begin{eqnarray}T = \frac{1}{2}m\dot x^2\tag{2}\label{eq2}\end{eqnarray}
次に,位置エネルギー\(U\)について考えよう.重力による位置エネルギー\(U_g\)は,
\begin{eqnarray}U_g = mgx\tag{3}\label{eq3}\end{eqnarray}
となり,ばねによる位置エネルギー\(U_k\)は,
\begin{eqnarray}U_k = \frac{1}{2}k x^2\tag{4}\label{eq4}\end{eqnarray}
となるので,全位置エネルギー\(U\)は下式になります.
\begin{eqnarray}U = U_g + U_k = mgx + \frac{1}{2}k x^2\tag{5}\label{eq5}\end{eqnarray}
散逸エネルギー\(F\)は下式になります.
\begin{eqnarray}F = \frac{1}{2}b \dot x^2\tag{6}\label{eq6}\end{eqnarray}
式\eqref{eq2}\eqref{eq5}\eqref{eq6}をラグランジュの運動方程式\eqref{eq1}に代入すると,
\begin{eqnarray}\frac{d}{dt} \left( \frac{\partial}{\partial \dot x}\left( \frac{1}{2}m\dot x^2\right )\right )-\frac{\partial}{\partial x}\left( \frac{1}{2}m\dot x^2\right )+\frac{\partial}{\partial \dot x} \left( \frac{1}{2}b \dot x^2 \right)+\frac{\partial}{\partial x}\left( mgx + \frac{1}{2}k x^2 \right )= f\tag{7}\label{eq7}\end{eqnarray}
となり,下式の運動方程式を導出できます.
\begin{eqnarray}m \ddot x + b \dot x + k x + mg = f\tag{8}\label{eq8}\end{eqnarray}
2.3 まとめ
今回の例では,ラグランジュの運動方程式を用いるよりも,ばねやダンパに生じる力を考えて運動方程式を算出する方が簡単かもしれません.しかし,運動・位置・散逸エネルギーを求め,ラグランジュの運動方程式\eqref{eq1}に代入するだけで,運動方程式を機械的に導出できました.この方法は複雑な対象でも同じ手順で機械的に運動方程式を導出できます.これがラグランジュの運動方程式の魅力です.