ラグランジュの運動方程式を用いるときに用いる,代表的なエネルギーをまとめます.
3.1 並進運動の運動・位置・散逸エネルギー
下図のように,垂直平面に質量\(m\)の質点に剛性\(k\)のばねと粘性\(b\)のダンパが付いている場合を考えよう.また質点には変位\(x\)が生じるとします.質点には,ばねにより変位\(x\)に比例して力\(kx\)が加わり,ダンパにより速度\(\dot x\)に比例して力\(b \dot x\)が加わると仮定します.
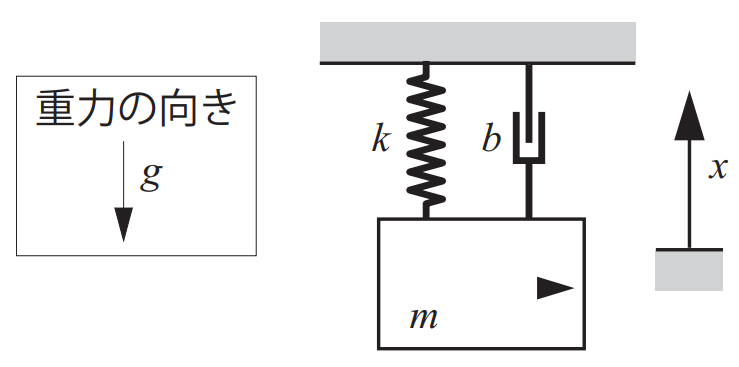
運動エネルギー\(T\),重力による位置エネルギー\(U_g\),ばねによる位置エネルギー\(U_k\)は高校のときに学んだ通りで,それぞれ\(T=(1/2)m\dot x^2\),\(U_g=mgx\),\(U_k=(1/2)kx^2\)になります.ダンパの粘性\(b\)により失うエネルギーを散逸エネルギー\(F\)と呼び,\(F=(1/2)b \dot x^2\)になります.
3.2 回転運動の運動・位置・散逸エネルギー
下図のように,慣性モーメント\(I\)の円板にねじり剛性\(k\)のばねと粘性\(b\)のダンパの要素が含まれている棒が付いている場合を考えよう.また円板には角度\(\theta\)が生じるとします.円板には,ばねにより角度\(\theta\)に比例してトルク\(k \theta\)が加わり,ダンパにより角速度\(\dot \theta\)に比例してトルク\(b \dot \theta\)が加わると仮定します.
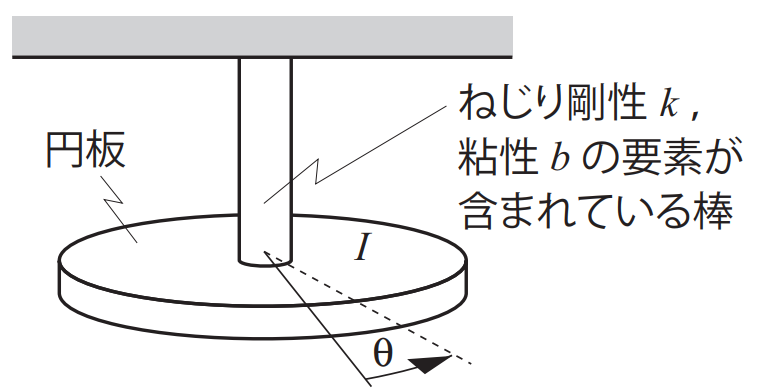
運動エネルギー\(T=(1/2)m\dot \theta^2\),位置エネルギー\(U=(1/2)k \theta^2\),散逸エネルギー\(F=(1/2)b \dot \theta^2\)になります.
3.3 まとめ
並進運動と回転運動の運動・位置・散逸エネルギーを下記の表にまとめます.
| 並進運動 | 回転運動 | ||
|---|---|---|---|
| ばねによる位置エネルギー | \(\frac{1}{2}k x^2\) | ばねによる位置エネルギー | \(\frac{1}{2}k \theta^2\) |
| 重力による位置エネルギー | \(mgx\) | ||
| 散逸エネルギー | \(\frac{1}{2}b \dot x^2\) | 散逸エネルギー | \(\frac{1}{2}b \dot \theta^2\) |
| 運動エネルギー | \(\frac{1}{2}m \dot x^2\) | 運動エネルギー | \(\frac{1}{2}I \dot \theta^2\) |
並進運動,回転運動の位置・散逸エネルギーにおいて,同じ\(b\),\(k\)を用いていますが,異なる物理量ですので単位は異なります.