ラグランジュの運動方程式は対象の運動をさまざまな座標にて表現できます.しかし,対象を動かす力やトルクのことを考えると適切な座標を選んだ方が後で混乱を避けることができますので,その注意点を解説します.
4.1 一般化座標
対象の運動を表現する座標は直交座標だけではありません.極座標や相対座標の方が便利なこともあります.具体的に下図のように直交座標\((x,y)\)と極座標\((r,\theta)\)について考えてみましょう.極座標\((r,\theta)\)は直交座標変数\(x\),\(y\)を用いて,\(r=\sqrt{x^2+y^2}\),\(\theta=\mathrm{tan^{-1}}\frac{y}{x}\)と表現できます.つまり,この座標は直交座標変数の間に1対1対応の関係があります.このような座標系を総称して一般化座標と呼びます.そして一般化座標は同じ次元である必要はありません.先ほど考えた極座標では\(r\)は変位で,\(\theta\)は角度ですので,同じ次元になっていませんが問題ありません.
このような説明では,一般化座標は「好みの座標を自由に選んで良いのかな?」のように考えるかと思います.結論から述べると,ロボットに適応する場合,ロボットを動作させる力やトルクを,一般化座標に対応した一般化力に変換できるのであれば好みの座標を自由に選んでも問題ありません.しかし,この変換は人間の直観では理解できないことが多くあり,混乱を招く原因になりますので,とりあえずは変換しなくてもよい一般化座標を選ぶことをお勧めします.
4.2 一般化力
下図のように3つのリンクによって構成されたロボットアームを考えよう.ここでリンクの角度を一般座標として,(a)は水平面から座標\((\phi_1,\phi_2,\phi_3)\)を定義し,(b)は相対角度を座標\((\theta_1,\theta_2,\theta_3)\)として定義します.このとき(a)(b)の一般化座標における一般化力(ここではトルクになります.)1をそれぞれ\((\omega_1,\omega_2,\omega_3)\),\((\tau_1,\tau_2,\tau_3)\)とします.さて,これらにはどのような違いがあるのでしょうか?
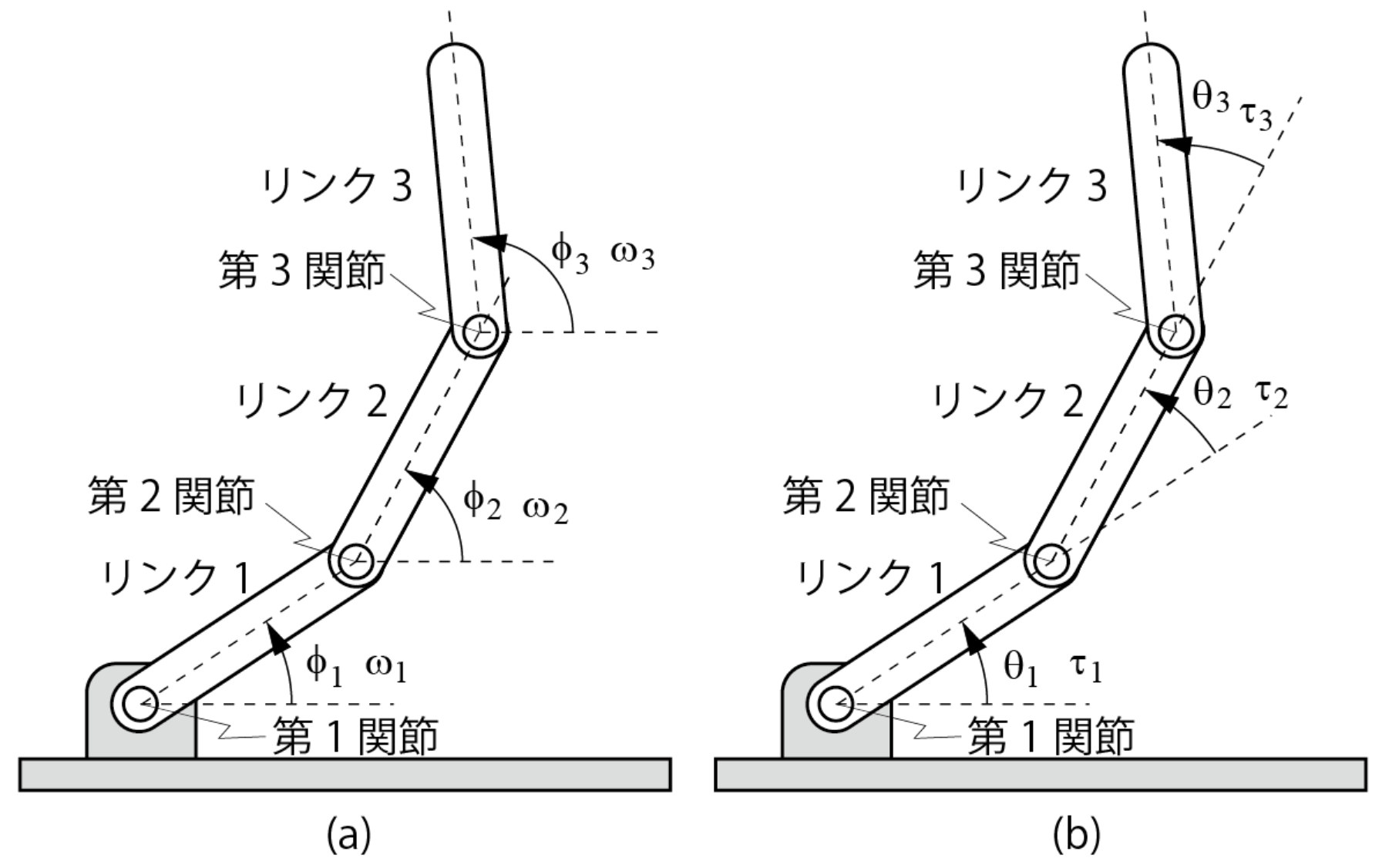
図4.2.1 一般化座標と一般化力
一般化座標の取り方の違いにより生じる,一般化力の違いをロボットの中の人で表現すると下図のようになります.(a)は地面と同様に動かない水平面から座標を定義していますので,一般化力も地面からそれぞれのリンクに加えたトルクが表現されます.(b)は地面とリンク1,リンク1とリンク2,リンク2とリンク3のように関節の前後の対象との相対角度を座標として用いています.そのため,一般化力も同様にそれぞれの間のリンクに加えたトルクが表現されます.ここで,どちらの座標を使うべきか悩む場合は,アクチュエータがどのように配置されているかを考えてください.
もう少し一般的に説明すると,対象aの上にアクチュエータが実装され,対象aから対象bを駆動しているとします.このとき,一般化座標に対象aと対象bの相対座標を選べば,一般化力は対象aと対象bの間に加えたものになります.
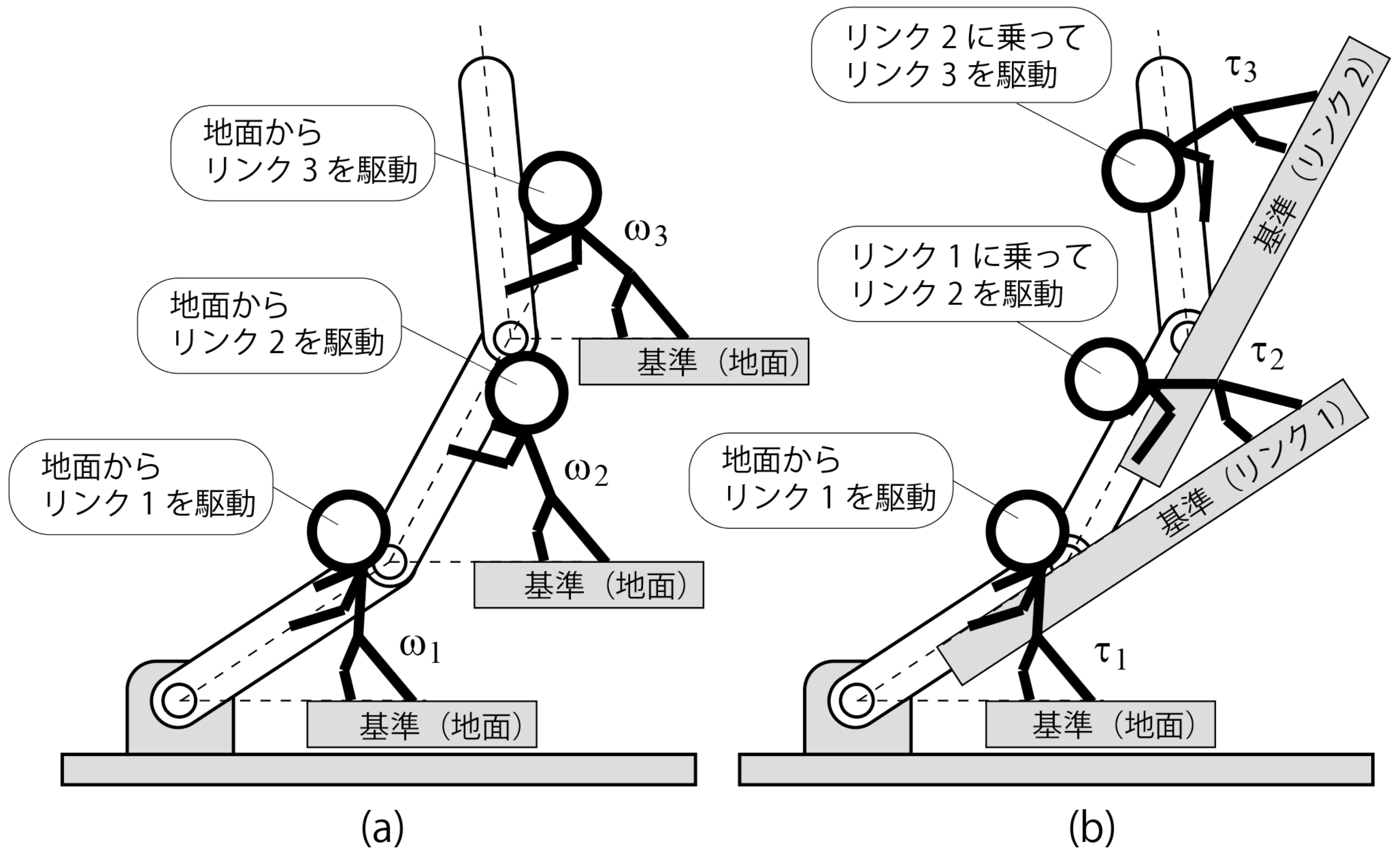
図4.2.2 一般化力をロボットの中の人で表現
4.3 まとめ
ラグランジュの運動方程式を用いて運動方程式を導出する場合,一般化座標を定める必要があります.そして,よく混乱するのが一般化力です.今回はロボットの例を示して,一般化座標と一般化力の関係について説明しました.実際にロボットの運動方程式を導出するのであば,モータなどのアクチュエータがどのように実装されているかを考えながら,これらの関係を定めるのがよいでしょう.
- 一般化座標が変位の次元のとき一般化力は力の次元となり,一般化座標が角度の次元のとき一般化力はトルクの次元になります. ↩︎